【广义凸集】
拼译：generaliged convex sets
设X是实线性空间，对x，y∈X，记［x，y］=｛z｜z=λx+(1－λ)y，λ∈［0，1］｝，称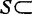
X是凸集，如对
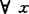，y∈S有
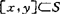。虽然凸集的某些结论可以追溯到18世纪中叶，但近代凸集理论则是20世纪初由卡拉什多利(C．Carathedory)、闵科夫斯基(H．Minkowskii)等人开创的，他们对集合的凸包、凸集的支撑、分离等问题进行了研究，为凸集理论的建立奠定了基础。以后由于赫里(E．Helly)、克里(V．L．klee)、哥德曼(J．Goldman)等一大批数学家的努力，到20世纪50年代凸集理论已基本形成。由于凸集理论在纯数学、应用数学、经济学等学科中得到广泛应用，所以它一直为人们所注目。同时人们也注意到实际问题中的许多集合不具备凸性，而只有某种类凸性，这就促使一些学者针对所研究问题的需要，提出了许多减弱凸性要求的广义凸集概念。
，
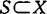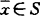；称S在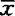
局部凸，如对
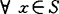，有
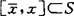；称S在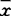
强局部凸，如存在
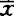的邻域N，使S∩N是凸集；称S在
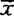弱局部凸，如存在
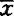的邻域N，对
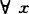，y∈S∩N，有
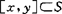，并得出了狄茨定理：一个闭连通集S是凸的，当且仅当S是弱局部凸的。一个连通的弱局部凸集必是折线连通的。以后克依(D．C．Kay 1971和1982)又对狄茨定理作了进一步推广。另外依温(G．Ewing，1977)又将S在
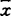局部凸拓广为S在
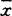局部星状，如对
，
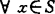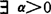使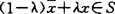
，
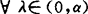。这概念在不可微最优化问题的讨论中常用到。1946年，M．A．Krasnosel’skii在考虑公共可见点问题时，称
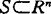是星形的，如
使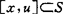
，
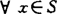，借用这概念得出了一个赫里型的艺术画廊定理：若S是Rn中至少含有n+1个点的紧集，又对S的每n+1个点x0，x1，…，xn都存在一个可见点y(即
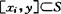，i=0，1，…，n)，则集合S是星形的。1974年，P．L．Yu在讨论多目标最优化问题的非控解时引进了一种锥凸性概念，他称
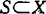关于d∈X是方向凸的，如对
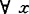，y∈S，λ∈［0，1］，
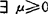使λx+(1－λ)y+μd∈S；对X中的凸锥C，称S是C－方向凸的，如对
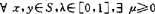使λx+(1－λ)y+z∈S；称S是C－凸的，如S+C是凸集。以后在一些多目标最优化方面的文献中又出现了一些更弱的锥凸性概念，如赵(K．L．Chew，1984)称S是C－凸的，如
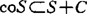，其中coS是S的凸包。布勒栅(A．Bressan，1987)称S是C－凸的，如x，y∈S，x－y∈C，蕴涵
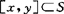。梅家骝(1988)称S是弱C－凸的，如存在集合A使
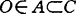，且S+A是凸集。1976年，V．G．Boltyanskii提出了一种H－凸性概念，1981年索坦(V．P．soltan)将其扩充为：设H是Rn的单位球面上的一个子集，称
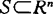是H－凸的，如果它是一族外法线属于H的开半空间的交。他对这种H－凸集的一些一般的性质进行了讨论。1979年，J．Szczepaniak，设0＜S≤1，称集合
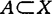是S凸的，如对
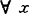，y∈A，a，b≥0，aS+bS=1，有ax+by∈A。相应地定义f：A→R为S－凸函数，如f(ax+by)≤asf(x)+bSf(y)，每当x，y∈A，a，b≥0，aS+bS=1。他将凸函数不等式的一些性质拓广到S－凸函数。1983年，J．P．Vial设r＞0，B(x，r)是赋范线性空间X中以x为中心，r为半径的闭球，Rr=｛B(x，r)｜x∈X｝，对x，y∈X，‖x－y‖≤2r，记Dr(x，y)=∩｛B｜B∈Rr，x，y∈B｝，称
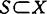关于r弱凸，如对
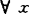，y∈clS，‖x－y‖＜2r有Dr(x，y)∩clS≠｛x，y｝，称S弱凸，如
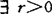，使S关于r弱凸。称S在
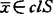局部弱凸，如
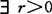，ε＞0使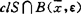
关于r弱凸。他还引进了强凸集的概念，讨论了强(弱)凸集的性质，其中特别是引进了支撑球的概念，它是支撑超平面概念的拓广。1984年，I．Marugsciao引进一种弧式凸性，称
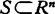是m－多角形凸的，如对
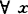，y∈S，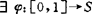
使φ(0)=x，φ(1)=y且存在0=t1＜…＜fm=1使
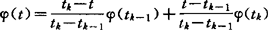，t∈［tk－1，tk］。相应地还定义了m－多角形凸(拟凸，伪凸)函数，讨论了这类广义弧式凸函数的极值性质。梅家骝(1981)在讨论多目标非控点的性质时，曾引进一类锥弧式凸性，对
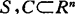，称S是弧式C－凸(严格凸)，如对
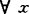，y∈S，存在φ：［0，1］→S，使φ(0)=x，φ(1)=y，对
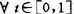有a=(1－t)x+ty－φ(t)∈C(且
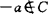)。称S弧式C－拟凸，如对
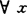，y∈S，存在φ：［0，1］→S，φ(0)=x，φ(1)=y且对
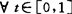有x－φ(t)∈C或y－φ(t)∈C。讨论了锥弧式凸性的基本性质。1985年，A．Aleman称
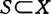弱凸，如对
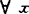，y∈S，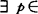
(0，1)使(1－p)x+py∈S，若有某个p不依赖x，y，则称S是p－凸的，特别如
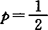，称为中点凸的。1987年狄可夫(M．P．DymkoV)定义另一种p－凸性，设ai∈Rn，i=1，…，m，称
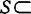Rn是p－凸的，如对
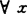，y∈S，λ∈［0，1］，
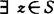使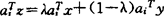
，i=1，…，r，
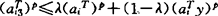，i=r+1，…，m，其中p是使上述关系式成立的最小自然数，文中讨论了这类p－凸集的极小点的必要和充分条件。1988年梅家骝从区域规划、场地设置的角度出发，提出了一类广义凸集概念，称
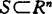是伪(严格伪)凸集，如存在凸集A，闭集(紧集)B，使S=A＼B，若其中A是凸锥，又称S是伪(严格伪)凸锥。称S拟凸，如对
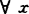，y∈S，(x，y)∩S在(x，y)中稠密；称S弱拟凸，如对
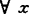，y∈S，(x，y)∩S≠Φ；称S强拟凸，如对
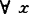，y∈S，(x，y)中最多有有限个点不属于S。称S为拟锥，若对
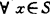，｛λx｜λ≥0｝∩S在｛λx｜λ≥0｝中稠密；称S为拟凸锥，如S既是拟锥又是拟凸集。系统地讨论了这类广义凸集(锥)的运算性质、射影定理、支撑定理、分离定理、相对内部的特征。1989年又讨论了这类广义凸集的支撑函数、退化锥、障碍锥的性质。1990年考虑了这类广义凸集的九种切锥的基本性质以及各种切锥之间的关系。1991年考虑了伪凸集的Pareto有效极点的存在性。1989年郭元明等将这类广义凸集拓广到赋范线性空间X，考虑了弱拟凸集
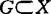对x∈X的最佳逼近和G对有界集
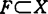的联合最佳逼近的唯一性，说明在严格凸赋范线性空间中的弱拟凸集均为半－切比雪夫集合。1992年郭元明又将前面所得结果应用到Lp(T．m)空间，得到了L1(T，m)空间中最佳逼近的特征及唯一性，Lp(T，m)(1＜p≤2)空间中最佳逼近的强唯一性。徐士英(1990)说明了伪凸集、拟凸集与太阳集之间的关系。【参考文献】：1 Szczepaniak J. Funct Approx Comment Math, 1979,7:3-72 Soltan V P. Dokl Akad Nauk SSSR,1981,258|1095～10623 Kay D C. Discrete geometry and convexity. New York,1982,170～1914 Vial J P. Math Oper Res 1983,8:231～2595 Marugsciac I. Polygonal convex functions, Ma thematica(cluj),1984,26:53～646 Aleman A. Anal Numer Theor Approx,1985,14:1～67 Bressan A. J Math Anal Appl, 1987,1:234～2468 Dymkov M P. Vestsi Akad Navuk BSSR Ser Fiz-Mat Navuk, 1987,125:20～259 梅家骝．系统科学与数学，1988，8∶97～10610 郭元明．系统科学与数学，1992，12∶30～34(南昌大学梅家骝教授撰；李宗元审)