【黎曼流形特征值的估计】
拼译：estimation of the eigenvalue of a manifold Riemannienne
谱几何正问题的一个重要研究课题是计算流形的谱。通常直接算出流形的谱是十分困难的，为此要对特征值(即谱值)进行估计，找出其下控与上界。此问题引伸到等周不等式的探讨，以及Pinching问题的研究，此外，在物理学中，确定鼓膜的形状也需用特征值的计算。
设(M，g)是紧致、连通的黎曼流形，则黎曼流形(M，g)的谱：Spec(M，g)=｛λ∈R｜△f=λf，λ≠0，f∈C∞(M)｝，
这里△是作用在C∞(M)上的Laplace算子。Spec(M，g)=｛0=λ0＜λ1＜λ2＜…∞｝
黎曼流形(M，g)的剖分函数Z(t)定义为Z(t)=Σmie↑（－λit，这里mi为特征值的λi的重数。由Z(t)可决定(M，g)的谱值和其重数。Minakshisundaram-Pleijel于1949年得到剖分函数的渐近展开式：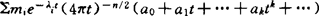
，这里ak是黎曼不变量。实际上是流形M的曲率张量与其各阶共变导数的函数。根据Mckean-Singer引入的正交不变量方法，可得到a0=vol(M，g)，
，
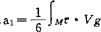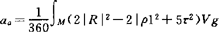，这里τ是数量曲率，ρ是Ricci曲率，R是黎曼曲率。a3已由T．Sakai于1971年算出，而当k≥4时，ak几何意义至今尚不知。第1个非零特征值λ1的计算，不仅在谱几何研究中具有一定的理论价值，而且在鼓膜振动和波方程中也具有应用价值，A．Lichnerowicz于1958年指出：设(M，g)，是一个n维紧致的黎曼流形，若存在正数k＞0，使得ρ≥kg，其中ρ为Ricci张量，则△的第1个非零特征值λ1，满足
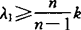。它的逆定理就是M．Obata于1962年建立的Obata定理：设(M，g)是一个n维紧致的黎曼流形，若存在正数k＞0，使得ρ≥kg，并且
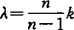，则(M，g)与(Sn，g0)等距。J．Cheeger于1970年得到λ1的极小值原理：
这里H1(M)是与1正交的一切C1函数所构成的空间。如果采用范数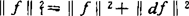
，则H1(M)关于范数‖f‖1是完全的。J．Cheeger于1968年得到λ1的上界：如果对于任一自然数n，存在一数h(n)≥0，使得n维紧致黎曼流形(M，g)的截面曲率大于或等于0，则λ1≤h(n)×［diam(M，g)］2。在此，依赖于n的h(n)如何选择为最佳?曲率非负的条件能否去掉，这一切有待于进一步改正。Cheeger定理的证明与流形(M，g)上一点m的割迹C(m)密切相关，而割迹的研究又同闭测地线的性质相联系，为此，闭测地线理论与割迹性质的研究推动了谱几何学科向纵深发展。
这是M．Berger于1970年建立的，本结果的证明需用Morse临界点理论。至于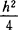
是否为λ1的最好下界?这个问题至今尚未解决。此外，对第2个非零特征值λ2是否有估算的必要?如果要进行计算，其下控与上界又是如何?这一切问题既难而有趣。
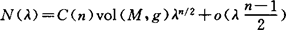，认为这个估计是最佳的。1975年J．Duistermat和V．Guellemen认为R(λ)=N(λ)－C(n)vol(M，g)λn／2与(M，g)测地线流关系密切。粗略地说，R(λ)为
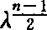阶当且仅当(M，g)的测地线流是周期的，即所有测地线是具有相同周期的闭测地线。例如，球面Sn上所有测地线是以2π为周期的周期测地线。同样可粗略地说：如果测地线流不是周期的，则
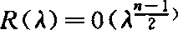。1976年P．Berard和B．Randol，对于负曲率流形证明
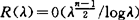。一般对R(λ)的研究是较为困难的，它要用数论知识。对带有边界的流形，困难就更大了。然而为了计算、估计流形的谱，这一领域的工作仍是一个研究热点。【参考文献】：1 Obata M.J Math Soc Japan, 1962,142 Cheeger J. Archiv Der Math, 1968,193 Urakawa H. Proc Japan Acad,1977,534 Li P,Zhong J Q. Invent Math,1981,655 Berard P. IMPA(南京大学马传渔教授撰；莫绍揆审)